Geometry



| EXAMPLES || MCQs |
« Previous Chapter Next Chapter »

GEOMETRY

Geometry is a branch of mathematics concerned with shape, size, measurement, properties and relationships of points, lines, angles, surfaces and volume. In Geometry we will learn mainlly two types of figures 1. two-dimensional(2D) and 2. three-dimensional(3D). In 2D figure we have Triangles, Quadrilaterals and Circles and in 3D figure we have Cuboid, Cube, Right Circular Cone, Cylinder and Sphere. To know the details click below :
These are Two Dimensional (2D) Figures :

TRIANGLE

A triangle is a polygon with three angles and three sides. It is one of the basic shapes in geometry. A triangle with sides A, B, and C is denoted by Δ ABC.

Properties of Triangle :

The sum of the angles of a triangle is 180°.

The sum of any two sides of a triangle is greater than the third side.

Types of Triangle :

1. Right-Angle Triangle :

Pythagoras Theorem : In a Right-angle Triangle.

(Hypotenuse)2 = (Base)2 + (Height)2.

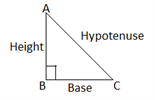
Triangle

Area of a Right-angle triangle : Triangle3

Triangle1

Perimeter of a triangle : Sum of all sides = (x + y + z)

2. Equilateral Triangle : 

If each side and each angle(i.e 60°) of a Triangle is equal, then it is called an Equilateral Triangle. 

Equilateral

Formulas :

Area of Equilateral Triangle : √3/4 × (side)2 = √3/4 × (a)2

Perimeter of Equilateral Triangle : 3 × side = 3 × a = 3a

3. Any Triangle :

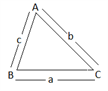
Any Triangle

Formula :

Area of Any Triangle : Any Triangle1[where S = Semi Perimeter,Any Triangle1]

QUADRILATERAL

A Quadrilateral is a Polygon with four sides and four angles. The sum of all angles is 360°.

Types of Quadrilateral :

1. Square : A Quadrilateral, in which all sides are equal and opposite sides are parallel to each other and each angle is equal and 90°, called a Square.

Square

ABCD is a square

AB = BC = CD = DA = a

Square1

Diagonal, AC = BD

Formulas :

Area of a Square : (side)2 = a2.

Perimeter of a Square : Sum of all sides = 4a.

Diagonal : √(a2 + a2) = a.√2

2. Rectangle : A Quadrilateral, in which opposite sides are equal and parallel and angle is 90°, called a Rectangle.

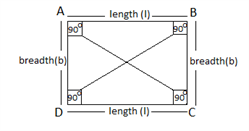
Rectangle

ABCD is a Rectangle

AB = DC = length = l

AD = BC = breadth = b

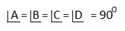
Square1

Diagonal, AC = BD

Formulas :

Area of a Rectangle : (length × breadth) = l × b

Perimeter of a Rectangle : Sum of all sides = l+b+l+b = 2l+2b = 2(l+b).

Diagonal : √ (l2 + b2)


3. Parallelogram : A Quadrilateral, in which opposite sides are equal and parallel, but the angles are not 90°, called a Parallelogram.

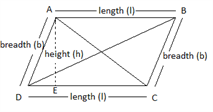
Parallelogram

ABCD is a Parallelogram

AB = CD = length = l (base)

AD = BC = breadth = b

AE = height = h

Diagonals, AC ≠ BD

Formulas :

Area of a Parallelogram : (base × height) = (l × h).

Perimeter of a Parallelogram : 2 × (length + breadth) = 2 × l × b.

Adjacent angle of A is B & D then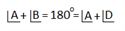Ab

4. Rhombus : A Quadrilateral, in which all sides are equal and parallel, but the angles are not 90°, called a Rhombus.

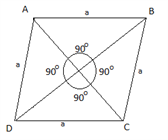
Rhombus

ABCD is a Rhombus

Let Diagonals AC = d1 and BD = d2 

Formula :

Area of a Rhombus : (AC × BD)/2 = (d1 × d2)/2


5. Trapezium : A Quadrilateral, in which two sides are parallel, called a Trapezium.

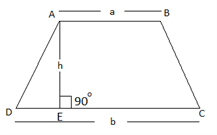
Trapezium

ABCD is a Trapezium

AB and CD are parallel sides and AE is distance between them

Let AB = a, CD = b and AE = h, then

Formula :

Area of a Trapezium : 1/2 × (sum of parallel side × distance between them) = 1/2 × (a + b) × h.

CIRCLE

A Circle is a round shaped figure that has no corners or edges and whose boundary consists of points equidistant from a fixed point (the centre).

Circle

This is a Circle, AO or OB = radius = r (let)

Then Diameter, AB = 2r

Formulas :

Area of a Circle : ∏r2, where ∏ = 22/7

Circumference of a Circle : 2∏r

Semi-Circle :

Area : 1/2 ∏r2

Circumference : 2∏r/2 + 2r = ∏r + 2r = r (∏ + 2)

Length of an arc AB : 2∏r/2 = ∏r

Sectorial Area of a Circle :

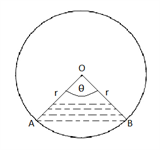
Circle1

Let,Ab1then
Area = ∏r2 × θ/360°
Length of an arc = 2∏r × θ/360°
Circumference of AOB = 2∏r × θ/360° + 2r
These are Three Dimensional (3D) Figures :

CUBOID

A cuboid is a 3-D shape. Cuboids have six faces and its each face is rectangular, which are placed at right angles. Each of the opposite faces are parallel and congruent. There are three pairs of parallel faces. Two adjacent faces join in a line segment called edge. There are twelve edges in a cuboid.

Cuboid

  • Surface Area of Cuboid : 2 (lb + bh +hl)
  • Diagonal of Cuboid : Cuboid1
  • Volume of Cuboid : Length × Breadth × Height = l × b × h

CUBE

A cube is a three-dimensional(3-D) solid object bounded by six square faces, which are placed at right angles. Each of the opposite faces are parallel and congruent. There are three pairs of parallel faces. Two adjacent faces join in a line segment called edge. There are twelve edges in a cube.

Cube

  • Surface Area of Cube : 6 × a2
  • Diagonal of Cube : a √3
  • Volume of Cube : a3

CONE

Cone

  • Slant Height of Right Circular Cone : Cone1
  • Curved Surface Area of Right Circular Cone : ∏rl
  • Total Surface Area of Right Circular Cone : ∏r2 + ∏rl = ∏r (r + l)
  • Volume of Right Circular Cone : 1/3 × (area of the base) × height = 1/3 ∏r2h

CYLINDER

Cylinder

  • Curved Surface Area of Cylinder : Perimeter of the base × height = 2∏rh
  • Surface Area of Cylinder : Curved surface area + area of the base + area of the top = 2∏rh + ∏r2 + ∏r2 = 2∏rh + 2∏r2 = 2∏r (h + r)
  • Volume of the Cylinder : Area of the base × height = ∏r2 × h = ∏r2h

SPHERE

Sphere

  • Curved Surface Area of the Sphere : 4∏r2
  • Volume of the Sphere : 4/3 ∏r3