PERCENTAGE
PERCENT : Percent means in each hundredth. It is a fraction whose denominator is always 100. It's sign is %. x percent is written as x% or x⁄100.
Thus, 20% = 20⁄100
PERCENTAGE : X as a percentage (X × 100)% and X⁄Y as percentage (X⁄Y × 100)%.
Thus, 1 as a apercentage (1 × 100)% = 100%. And 1⁄2 as a apercentage (1⁄2 × 100)% = 50%
SOME IMPORTANT FORMULAS :
RESULT ON COMMODITY :
- If the price of a commodity increases by R%, then the reduction in consumption so as not to increase the expenditure is -
[ × 100 ]%
- If the price of a commodity decreases by R%, then the increase in consumption so as not to decrease the expenditure is:
[ × 100 ]%
RESULTS ON POPULATION :
The population of a city is P and let it increases at the rate of R% per annum :
1. Population after n years :
P(1 +  )n
2. Population n years ago :
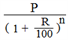
RESULTS ON DEPRECIATION :
Let P be the present value of a machine. Suppose it depreciates at the rate of R% per annum then
1. The value of the Machine after n years :
P(1 - )n
2. The value of the Machine n years ago :
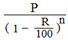
♦ If X is R% more than Y, then Y is less than X by
[ × 100 ]%
♦ If X is R% less than Y, then Y is more than X by
[ × 100 ]%
♦ Net change in percent(%) :
- X + Y +
 [when X% and Y% both are increase]
- X - Y - [when X% increase and Y% decrease]
- - X - Y + [when X% and Y% both are decrease]
|
