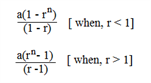NUMBERS
Digits : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Numbers : A number is denoted by a digit or a group of digits, called Numeral.
Values of numbers : In a numeral a digit has two values - (i) Place value and (ii) Face value.
(i) Place value : Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. Those positions start from a unit place or we also call it as one’s position. After units, it comes tens, hundreds, thousands, ten thousands, lakhs, ten lakhs and crores. So, place value of a number or digit means in which place the digit is placed.
- Place value of Unit Digit = (Unit Digit) × 1
- Place value of Tens Digit = (Tens Digit) × 10
- Place value of Hundreds Digit = (Hundreds Digit) × 100
- Place value of Thousands Digit = (Thousands Digit) × 1000
- Place value of Ten Thousands Digit = (Ten Thousands Digit) × 10000
and so on.
Place Value table :
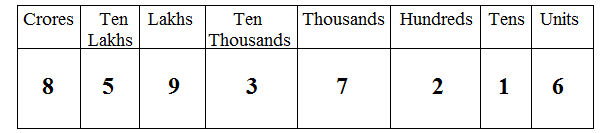
Here we have the numeral and that is 85937216
- Place value of Units Digit = 6 × 1 = 6
- Place value of Tens Digit = 1 × 10 = 10
- Place value of Hundreds Digit = 2 × 100 = 200
- Place value of Thousands Digit = 7 × 1000 =7000
- Place value of Ten Thousands Digit = 3 × 10000 =30000
(ii) Face Value : Place value in Maths describes its own value, at whatever place it may be.
Face value table :

Here we have the numeral and that is 85937216
- The face value of Units Digit = 6
- The face value of Tens Digit = 1
- The face value of Hundreds Digit = 2
- The face value of Thousands Digit = 7
- The face value of Ten Thousands Digit = 3
Types of Numbers
1. Natural Numbers - Counting numbers are called natural numbers. n > 0 where n is counting number. Thus 1,2,3,4,5,6,7..... are all natural numbers.
2. Whole Numbers - All the counting numbers and 0 form the set of whole numbers. n ≥ 0 where n is counting number. 0,1,2,3,4,5,6,..... all are whole numbers.
Note:
(i) 0 is the only whole number which is not a natural number.
(ii) Every natural number is a whole number.
3. Integers - All counting numbers, zero, negatives of counting numbers form the set of integers. n ≥ 0 or n≤0 where n is counting number; ..., -3, -2, -1, 0, 1, 2, 3... are integers. Thus, ...., -3, -2, -1, 0, 1, 2, 3, ....are all integers.
- Positive Integers - n > 0; Thus, 1,2,3,4,5...
- Negative Integers - n < 0; Thus, -1,-2,-3,-4,-5...
Note :
(i) 0 is neither positive nor negative integer.
4. Even Numbers - A counting number divisible by 2 is called an even number. n/2 and 0 where n is counting number. Thus, 0,2,4,6,8,10,12,... etc. all are even umbers.
5. Odd Numbers - A counting number not divisible by 2 is called an odd number. n/2 ≠ 0 where n is counting number. Thus, 1,3,5,7,9,11,13,... etc. all are odd numbers.
6. Prime Numbers - A Number which is divisible by itself and 1 only is called a prime number.
Note :
(i) 1 is not a prime number.
(ii) To test a number to be prime :
Let, p be a number and n be the smallest whole number such that n2 ≥ p. Get all prime numbers less than or equal to n and divide p with each of these prime numbers. If no number divides p exactly then p is a prime number otherwise it is not a prime number.
Example1: 137 is prime number or not ?
Solution:
We know that (12)2 =144
So, (12)2 > 137
Then, prime numbers less than 12 are : 2, 3, 5, 7 and 11.
Clearly none of them divides 137.
Therefore, 137 is a prime number.
Example2: 437 is prime number or not ?
Solution:
We konw that (21)2 = 441
So, (21)2 > 437
Then, prime numbers less than 21 are : 2, 3, 5, 7, 11, 13, 17, 19.
Clearly, 437 is divisible by 19.
Therefore, 437 is not a prime number.
7. Composite Numbers - Non-prime numbers > 1. For example, 4,6,8,9 etc.
Note:
(i) 1 is neither a prime number nor a composite number.
(ii) 2 is the only even prime number.
8. Co-Primes Numbers - Two natural numbers are co-primes if their H.C.F. is 1. For example, (2,3), (4,5) are co-primes.
Divisibility

1. Divisibility by 2 - A number is divisible by 2 if its unit digit is 0, 2, 4, 6 and 8.
Example1: 34474 is divisible by 2 or not ?
Solution:
4 is the Unit digit of 34474.
So, 34474 is divisible by 2.
Example2: 89753 is divisible by 2 or not ?
Solution:
3 is the Unit digit of 89753.
So, 89753 is not divisible by 2.
2. Divisibility by 3 - A number is divisible by 3 only when the sum of its digits is divisible by 3.
Example1: 96186 is divisible by 3 or not ?
Solution:
Sum of its digits is 9 + 6 + 1 + 8 + 6 = 30
Which is divisible by 3.
Therefore, 96186 is divisible by 3.
Example2: 219817 is divisible by 3 or not ?
Solution:
Sum of its digits is 2 + 1+ 9 + 8 + 1 + 7 = 28
which is not divisible by 3.
Therefore, 219817 is not divisible by 3.
3. Divisibility by 4 - A number is divisible by 4 when the number formed by its last two digits is divisible by 4.
Example1: 973128 is divisible by 4 or not ?
Solution:
Number formed by its last two digits is 28.
Which is divisible by 4.
Therefore, 973128 is divisible by 4.
Example2: 543218 is divisible by 4 or not ?
Solution:
Number formed by its last two digits is 18.
Which is not divisible by 4.
Therefore, 543218 is not divisible by 4.
4. Divisibility by 5 - A number is divisible by 5 if its unit digit is 0 or 5.
Example1: 34691 is divisible by 5 or not ?
Solution:
Unit digit is 1.
Therefore, 34691 is not divisible by 5.
Example2: 975865 is divisible by 5 or not ?
Solution:
Unit digit is 5.
975865 is divisible by 5.
5. Divisibility by 6 - A number is divisible by 6 if the number is divisible by both 2 and 3.
Example1: 512118 is divisible by 6 or not ?
Solution:
Unit digit is 8. So, number is divisible by 2.
Sum of its digits is 5 + 1 + 2 + 1 + 1 + 8 = 18.
which is divisible by 3.
Therefore, 512118 is divisible by 6.
Example2: 63892 is divisible by 6 or not ?
Solution:
Unit digit is 2. So, number is divisible by 2.
Sum of its digits is 6 + 3 + 8 + 9 + 2 = 28
which is not divisible by 3.
Therefore, 63892 is not divisible by 6.
6. Divisibility by 8 - A number is divisible by 8 when the number formed by its last three digits is divisible by 8.
Example1: 73278 is divisible by 8 or not ?
Solution:
Number formed by its last three digits is 278.
Which is not divisible by 8.
Therefore, 73278 is not divisible by 8.
Example2: 73184 is divisible by 8 or not ?
Solution:
Number formed by its last three digits is 184.
Which is divisible by 8.
Therefore, 73184 is divisible by 8.
7. Divisibility by 9 - A number is divisible by 9 if sum of its digits is divisible by 9.
Example1: 246591 is divisible by 9 or not ?
Solution:
Sum of its digits is 2 + 4 + 6 + 5 + 9 + 1 = 27.
Which is divisible by 9.
Therefore, 246591 is divisible by 9.
Example2: 734519 is divisible by 9 or not ?
Solution:
Sum of its digits is 7 + 3 + 4 + 5 + 1 + 9 = 29.
Which is not divisible by 9.
Therefore, 734519 is not divisible by 9.
8. Divisibility by 10 - A number is divisible by 10 if its unit digit is 0.
Example1: 298765 is divisible by 10 or not ?
Solution:
Unit digit is 5.
Therefore, 298765 is not divisible by 10.
Example2: 592640 is divisible by 10 or not ?
Solution:
Unit digit is 0.
Therefore, 592640 is divisible by 10.
9. Divisibility by 11 - A number is divisible by 11 if difference between the sum of digits at odd places and the sum of digits at even places is either 0 or is divisible by 11.
Example1: 29435417 is divisible by 11 or not ?
Solution:
Difference between sum of digits at odd places
And sum of digits at even places = (7 +4 + 3 + 9) - (1 + 5 + 4 +2) = (23-12) = 11
Which is divisible by 11.
Therefore, 29435417 is divisible by 11.
Example2: 57463822 is divisible by 11 or not ?
Solution:
Difference between sum of digits at odd places
and sum of digits at even places = (2 + 8 + 6 + 7) - (2 + 3 + 4 + 5) = (23-14) =9. Which is not divisible by 11.
Therefore, 57463822 is not divisible by 11.
Results on Series
Following are formulas for number series:
(i) (1+2+3+...+n) = (1/2)n(n+1)
(ii) (12+22+32+...+n2) = (1/6)n(n+1)(2n+1)
(iii) (13+23+33+...+n3) = (1/4)n2(n+1)2
(iv) Arithmetic Progression(A.P)
a, a+d, a+2d, a+3d, a+4d, ...... are said to be in A.P.
In which first term = a and common difference = d.
Let the nth term be tn and last term be l. Then,
I. nth term = a + (n-1) d
II. Sum of n terms = n/2 [2a +(n-1)d]
(v) Geometric Progression (G.P)
a, ar, ar2, ar3, .... are said to be in G.P.
In which first term = a and common ratio = r.
I. nth term = ar(n-1)
II. Sum of n terms =