Here are some solved examples of Number System :
Example 1. 1958 - ? = 736 - 5494
Solution :
Let, 1958 - x = 736 - 5494
or, 1958 - 736 + 5494 = x
or, x = 7452 - 736
or, x = 6716
Example 2. 2785698 × 999 = ?
Solution :
2785698 × (1000 - 1) = 2785698000 - 2785698 = 2782912302
Example 3. 7145 × 460 + 7145 × 540 = ?
Solution :
Let, 7145 × 460 + 7145 × 540 = x
or, x = 7145 × (460 + 540)
or, x = 7145 × 1000
or, x = 7145000
Example 4. 1540 × 1540 = ?
Solution :
1540 × 1540 = (1540)2 = (1500 + 40)2
= (1500)2 + 2 × (1500 × 40) + (40)2
= 2250000 + 2 × 60000 + 1600
= 2250000 + 120000 + 1600
= 2371600
Example 5. 1297 × 1297 = ?
Solution :
1297 × 1297 = (1297)2 = (1300 - 3)2 = (1300)2 - 2 × (1300 × 3) + (3)2
= 1690000 - 2 × 3900 + 9 = 1690009 - 7800
= 1682209
Example 6. (695 × 695 - 305 × 305) = ?
Solution :
(695 × 695 - 305 × 305) = (695)2 - (305)2
= (695 + 305) (695 - 305) [ (a2 - b2) = (a + b)(a - b)]
= (1000 × 390) = 390000
Example 7. What least number must be subtracted from 1942 to obtain a number which is completely divisible by 16 ?
Solution :
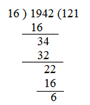
So, the number to be subtracted = 6
Example 8. What least number must be added to 1942 to obtain a number which is completely divisible by 16 ?
Solution :
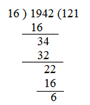
So, the number to be added = ( 16 - 6) = 10
Example 9. Simplify:
| 585 × 585 × 585 + 415 × 415 × 415 |
|
|
|
= |
? |
| 585 × 585 - 585 × 415 +415 × 415 |
|
|
Solution :
Example 10. what is the unit digit in the product (5389)134 × (361)27 ?
Solution :
9 is the unit digit of 5389 and 1 is the unit digit is 361
If we find the unit digit in the product (9)134 × (1)27
Then we will get the unit digit in the product (5389)134 × (361)27
91 gives unit digit 9 and 92 gives unit digit 1; and 127 gives unit digit 1
So, (9)134 × (1)27 =[(92)67 × 1]=[(81)67 × 1]
Therefore, required unit digit = [167 × 1] = [1 × 1] = 1
Example 11. How many natural numbers between 19 and 99 are divisible by 7 ?
Solution :
21, 28, 35, ....., 98. are the numbers which are divisible by 7.
This is in A.P. Where first term, a = 21; common difference, d = 7 and last term, l = 98.
Let the number of these terms be n. Then,
tn = 98
or, a + (n - 1)d = 98
or, 21 + (n - 1) × 7 = 98
or, (n - 1) × 7 = 98 - 21 = 77
or, (n - 1) = 77/7 = 11
or, n = 11 + 1 = 12
Therefore, 12 natural numbers between 19 and 99 are divisible by 7.
|